Trie Data Structure

An R-way Trie is a tree-like data structure, also known as a Prefix Tree or, more generically, a Digital Search Tree (DST)/Digital Tree. It is commonly used to implement string-based symbol-tables structures.

It has a certain resemblance to a binary-tree, but instead of having at most two children, each node can have multiple children (one for each character in the alphabet).

Structure

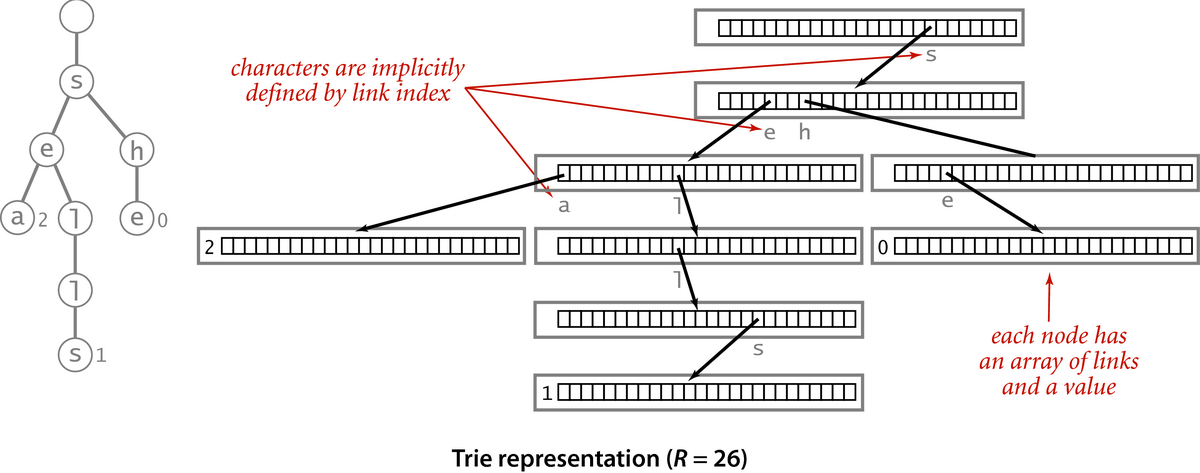
A trie consists of:

• Root node: Empty node that serves as the starting point
• Internal nodes: Each node represents a character
• Leaf nodes: Mark the end of a word
• Edges: Represent characters

Implementation

public class TrieNode
{
    public Dictionary<char, TrieNode> Children { get; set; }
    public bool IsEndOfWord { get; set; }
 
    public TrieNode()
    {
        Children = new Dictionary<char, TrieNode>();
        IsEndOfWord = false;
    }
}
 
public class Trie
{
    private readonly TrieNode _root;
 
    public Trie()
    {
        _root = new TrieNode();
    }
 
    public void Insert(string word)
    {
        var node = _root;
        foreach (char c in word)
        {
            if (!node.Children.ContainsKey(c))
            {
                node.Children[c] = new TrieNode();
            }
            node = node.Children[c];
        }
        node.IsEndOfWord = true;
    }
 
    public bool Search(string word)
    {
        var node = _root;
        foreach (char c in word)
        {
            if (!node.Children.ContainsKey(c))
            {
                return false;
            }
            node = node.Children[c];
        }
        return node.IsEndOfWord;
    }
 
    public bool StartsWith(string prefix)
    {
        var node = _root;
        foreach (char c in prefix)
        {
            if (!node.Children.ContainsKey(c))
            {
                return false;
            }
            node = node.Children[c];
        }
        return true;
    }
}

Operations

Insertion

Time Complexity: O(m) where m is the length of the word

public void Insert(string word)
{
    var node = _root;
    foreach (char c in word)
    {
        if (!node.Children.ContainsKey(c))
        {
            node.Children[c] = new TrieNode();
        }
        node = node.Children[c];
    }
    node.IsEndOfWord = true;
}

Search

Time Complexity: O(m) where m is the length of the word

public bool Search(string word)
{
    var node = _root;
    foreach (char c in word)
    {
        if (!node.Children.ContainsKey(c))
        {
            return false;
        }
        node = node.Children[c];
    }
    return node.IsEndOfWord;
}

Deletion

Time Complexity: O(m) where m is the length of the word

public void Delete(string word)
{
    DeleteHelper(_root, word, 0);
}
 
private bool DeleteHelper(TrieNode node, string word, int index)
{
    if (index == word.Length)
    {
        if (!node.IsEndOfWord)
        {
            return false;
        }
        node.IsEndOfWord = false;
        return node.Children.Count == 0;
    }
 
    char c = word[index];
    if (!node.Children.ContainsKey(c))
    {
        return false;
    }
 
    bool shouldDeleteChild = DeleteHelper(node.Children[c], word, index + 1);
 
    if (shouldDeleteChild)
    {
        node.Children.Remove(c);
        return node.Children.Count == 0;
    }
 
    return false;
}

Applications

1. Autocomplete: Suggest words as user types
2. Spell Checker: Check if words exist in dictionary
3. IP Routing: Longest prefix matching
4. Text Analysis: Word frequency and pattern matching

Advantages

• Fast prefix searches: O(m) time complexity
• Space efficient: Shared prefixes save memory
• Predictable performance: No hash collisions

Disadvantages

• Memory usage: Can be high for sparse data
• Cache performance: Poor locality of reference
• Complexity: More complex than hash tables

Related Concepts

• binary-tree - Similar tree structure with different branching
• symbol-tables - Used for implementing symbol tables efficiently